DC Parallel Circuits

Learn how parallel circuits work and how to calculate them. Scenario problems are also detailed at the end of this article for you to try and solve.

Scroll to the bottom to watch the YouTube tutorial.

What Are Parallel Circuits?

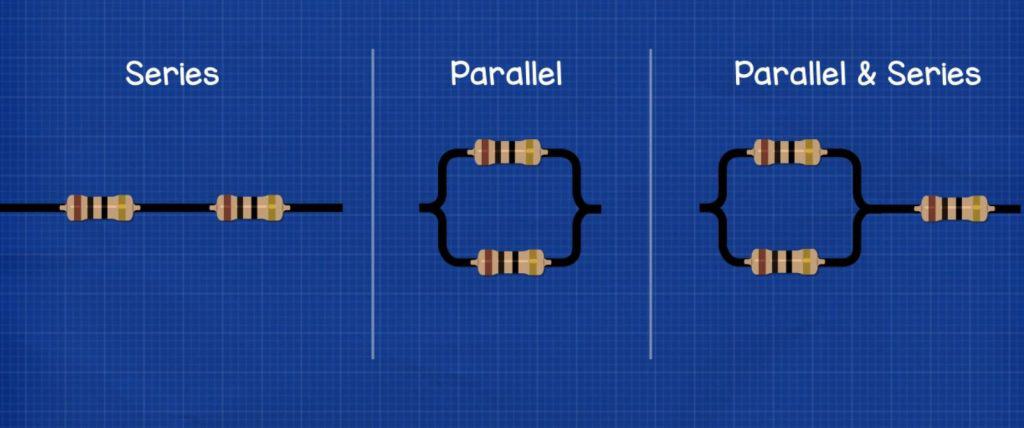
We can connect the components of a circuit in either series, parallel or a combination of series and parallel. 

When we place a lamp in series or parallel with a battery, the electrons will flow from the negative terminal of the battery, along the wire, through the lamp and then to the positive terminal of the battery.

In these animations we use electron flow which is from negative to positive but you might be used to seeing conventional flow which is from positive to negative. Electron flow is whats actually occurring. Conventional flow was the original theory and it’s still taught because it’s easier to understand. Just be aware of the two and which one we’re using.

How Does It Compare To Series Circuits?

In the series configuration; there is only one path for the electrons to flow along. If we place two lamps in a series circuit, they will both shine, but if one of the bulbs breaks then the entire circuit stops working because there is only one path to flow along. You might have seen this with strings of lights such as fairy lights. When one bulb pops, the whole string of lights stops working.

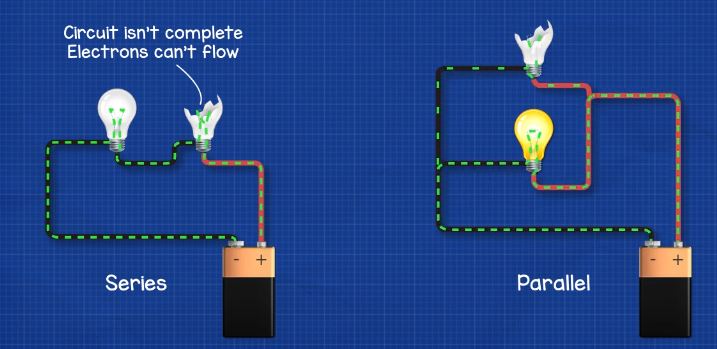
A solution to this is to wire the lamps in parallel. When we do this we provide the electrons multiple paths. If one lamp stops working the circuit will continue to work except for the broken path.

Voltage in parallel circuits.

Say we take a 1.5V battery, if we use a multimeter to measure across the two ends, we will read 1.5V. But if we measure the same end we get a reading of zero. Why? Because we can only measure the difference in voltage between two different points.

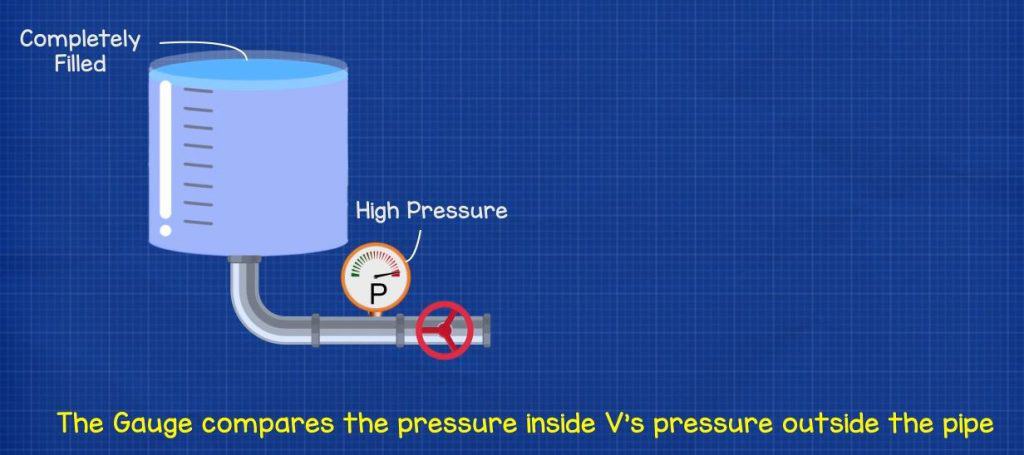
Voltage is like pressure in a water pipe. If you fill up the tank then the water pressure is high, we can read the pressure on a pressure gauge. The gauge is comparing two points, the pressure inside the pipe compared to the pressure outside the pipe, in order to know what the difference is. When the tank is empty the gauge reads zero because the pressure inside the pipe and outside the pipe are the same, so it has nothing to compare and is therefore zero.

The same with voltage. We can only measure the difference in voltage between two points. When we connect a component to a battery, it experiences the difference in voltage between the two points, or terminals, of the battery. The voltage or pressure will force the electrons to flow through the component. 

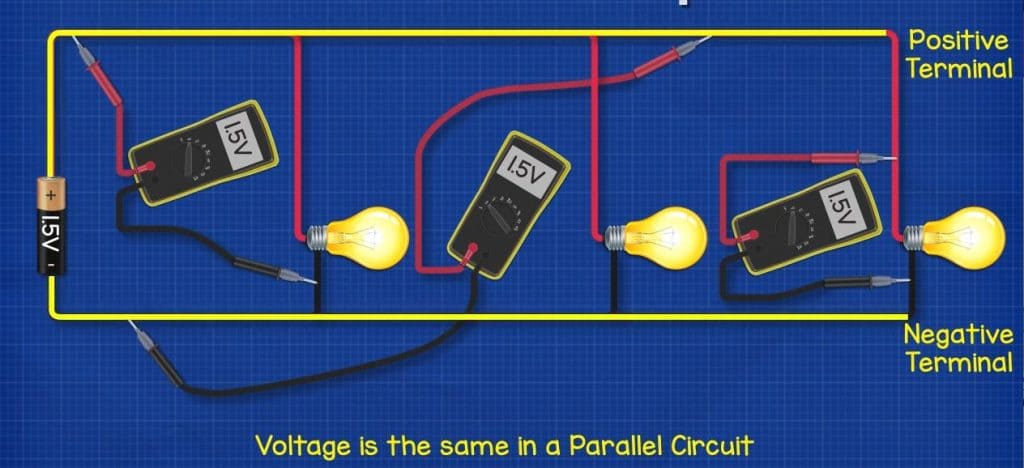
In parallel circuits the voltage is the same anywhere in the circuit. It doesn’t matter where we connect our multimeter- we get the same reading. Why? Because each component is connected directly to both the positive and the negative terminals of the battery so they receive the full pressure. In series circuits the components were connected to each other so the voltage reduced. But with parallel there are multiple routes and each is connected directly to the battery.

Voltage Formulas for Parallel Circuits

When we use voltage in the formulas for parallel circuits, its super easy because it’s the same value, it’s just the voltage of the connected battery.

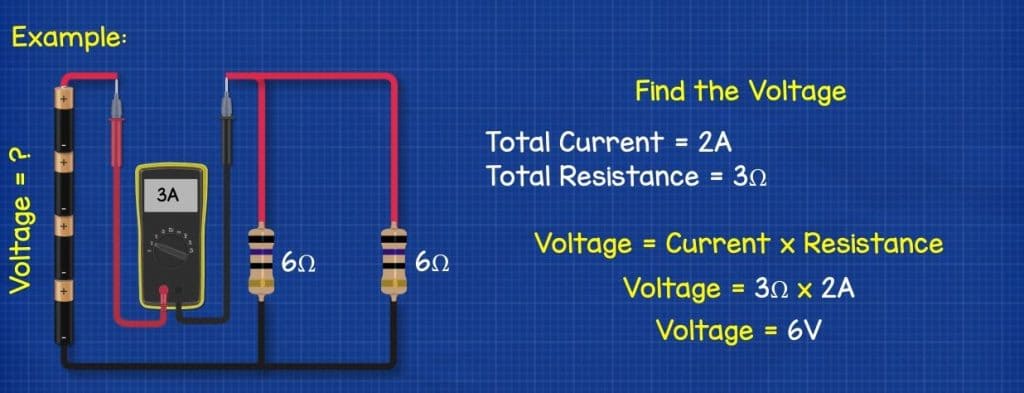
For example, In the circuit below; the total current is 2A and the total resistance is 3 ohms. What is the voltage of the battery? Well from ohms law we know we need the formula voltage = current multiplied by resistance so voltage equals 2A multiplied by 3 ohms which gives us 6 volts. 

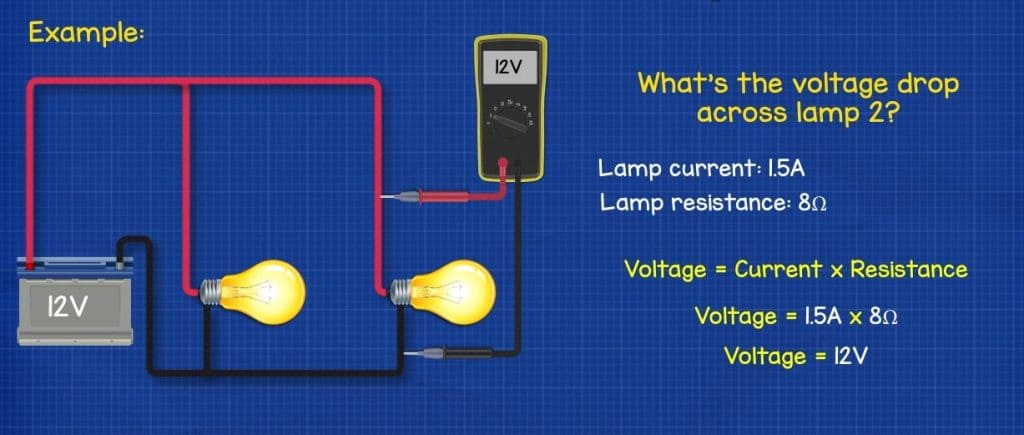
Another example, the circuit below is connected to a 12V battery. What is the voltage drop across the end lamp? Easy, we calculate voltage by again multiplying the current and the resistance. It has a current of 1.5A flowing through it and a resistance of 8 ohms. 1.5A multiplied by 8 ohms gives us 12V.

If we connected two 1.5V batteries in series, the voltage increases to 3V. The electrons are being boosted by the second battery so they increase in pressure or voltage.

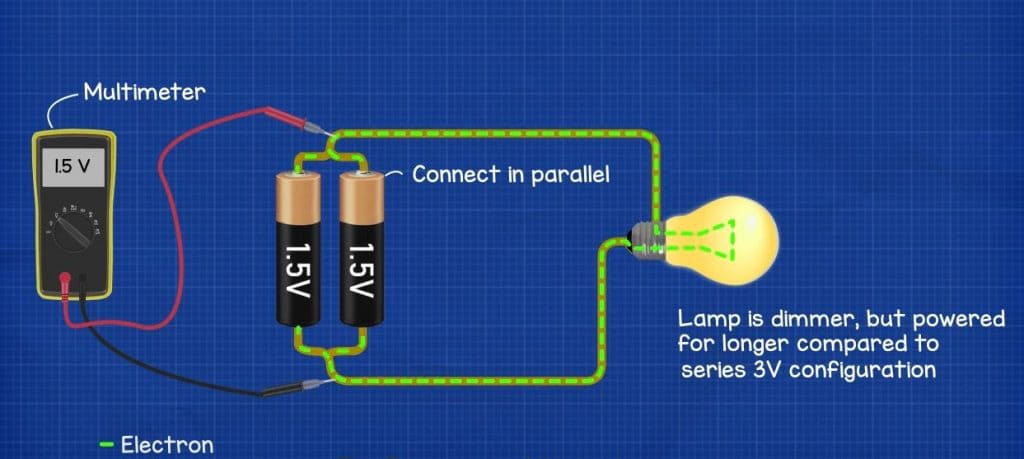
However, when we connect the batteries in parallel, the voltage doesn’t increase. We only get 1.5V. The batteries can’t boost each other in this configuration, the path for the electrons is joined and then split so the flow of electrons are shared between the batteries. The batteries therefore can’t provide more voltage, however their storage capacity has increased so they can provide 1.5V for longer than a single 1.5V battery by itself.

We’ve covered the basics of voltage in detail in a previous article; do check that out HERE.

Current flow in parallel circuits

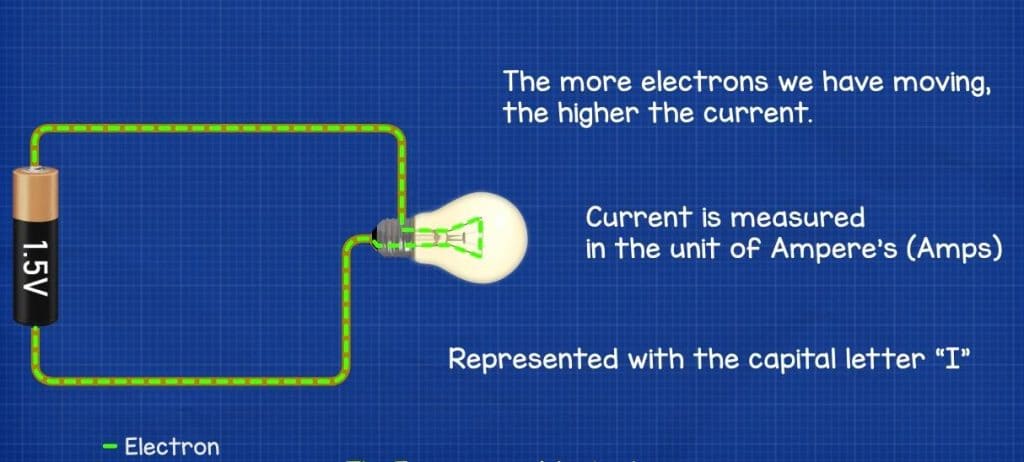
Remember current is the flow of electrons. We need electrons to flow in the same direction to power things like lamps. We apply a voltage difference across a component to force the electrons to move. As we apply more voltage, more electrons will flow. The speed of the electrons remains the same but the amount of electrons moving will vary. The more electrons we have moving, the higher the current. We represent current with the letter I and we measure current in the unit of ampere’s but we usually just shorten this to amps.

If we connect a lamp with a resistance of 1 ohm, to a battery rated at 1.5V the total current (It) in the circuit will be 1.5A. We can measure that by placing a multimeter into the circuit. Or, we can calculate that using Ohm’s law and the formula Current = voltage divided by resistance. 

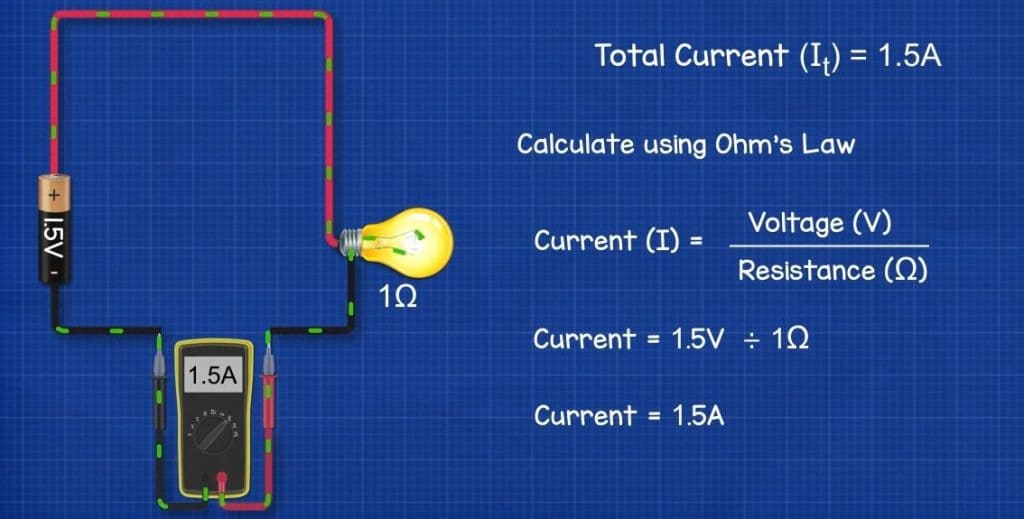
We’ve covered ohms law in detail in a previous article, do check that out HERE.

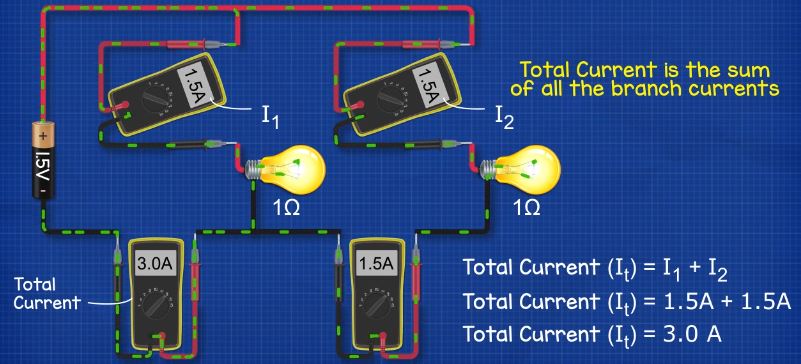
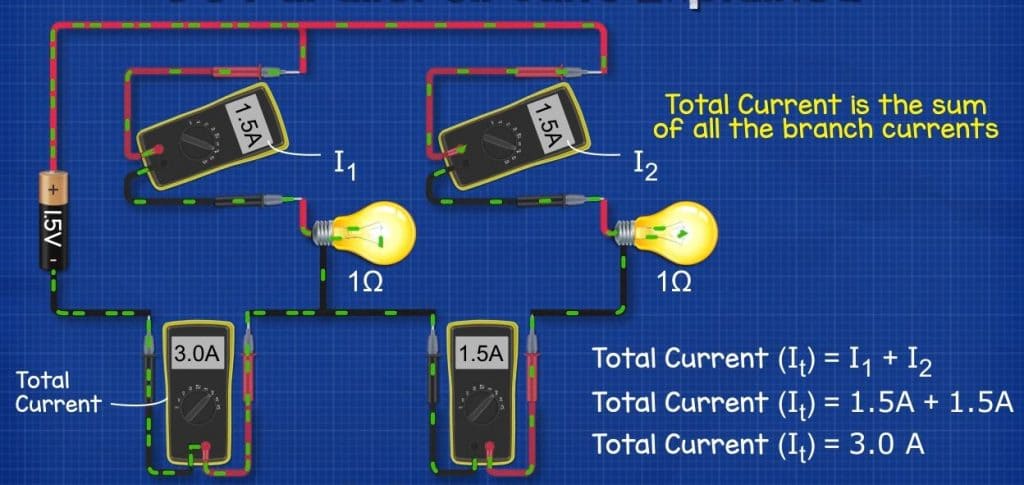
If we then connect a second 1 ohm resistive lamp into the circuit, wired in parallel. The multimeter reading the total current sees an increase to 3 Amps. But if we measure the current through the lamps individually, we see the multimeters will read 1.5A on each. In the wire between the two lamps we will also see 1.5A of current. So what’s happening here? We can see that the current will divide and the electrons will flow in all the different routes available to get back to the battery, they will then recombine. We can also see that the total current is the sum of the current in each branch. So we calculate the total current using the formula It = I1 + I2

If we replace lamp 1 with a 2 ohm resistive lamp, so that’s double the resistance on that branch, then the total current decreases to 2.25A, lamp 1 sees a current of 0.75A and will be less bright, lamp 2 continues to read 1.5A and the meter between lamp 1 and 2 continues to see 1.5A. Therefore we can see that the current flowing in each branch depends on the resistance of the branch and again, the total current in the circuit is the sum of the currents in each of the branches. It = I1 + I2

If we add a third 1 ohm lamp to the circuit and change lamp 1 back to 1 ohm also, so that’s 3x 1ohm lamps in parallel, we see the total current in the circuit is now 4.5A (It = I1 + I2 + I3) and each lamp continues to see just 1.5A of current. The multimeter on the wire between lamps 1 and 2 has increased to 3A but the meter between lamps 2 and 3 reads just 1.5A.

If we double the voltage from 1.5V to 3V the current will double too. The total current increases to 9A, the current between lamps 1 and 2 increases to 6A and each lamp now experiences 3A of current.

So from this we can see that the voltage applied will vary the current. The total current also varies with the resistance of each branch and how many branches are connected. 

Lets see some more detailed explanations on how to calculate this, see if you can solve it before we do. First lets try an easy one. Let’s find the total current.

Calculating The Total Current

Take a simple parallel circuit with 2 resistors and a 12V battery. Resistor 1 is 15 ohms and has a current of 0.8A flowing through it. Resistor 2 is 24 ohms and has a current of 0.5A flowing through it. What will the multi-meter read for the total current in the circuit?

Well we know that the total current in the circuit is equal to the sum of currents in all the branches. Therefore 0.8A + 0.5A is 1.2A of current in total.

What if we know the total current and the current in one branch, how do we find the current in the other branch? Easy, we just subtract. So in this example we have a 12v battery connected to two resistors. The total current is 3A and branch one has a current of 1.8A. The current in branch two is therefore 3A subtract 1.8A which gives us 1.2A.

How do we calculate the current in a simple branch? We use the formula Current = Voltage divided by resistance. Lets say we have three resistors wired in parallel to a 6V battery. Resistor one is 10 ohms, resistor two is 2 ohms and resistor three is 5 ohms. What’s the current flowing through each?

Well lets look at resistor one first, current equals voltage divided by resistance. So 6V divided by 10 ohms gives us 0.6A. Resistor 2 is 6V divided by 2 ohms which is 3A and resistor three is 6V divided by 5 ohms which is 1.2A, So the current in this part will be 1.2A because there’s only the current from the single resistor. The current in this wire will be 4.2A because there’s the current of resistor two and three passing through it. The current here is the total current which is 4.8A because the current for all three branches flows through it.

Total resistance in a parallel circuit

This is the part which people struggle with the most, it looks difficult because of the formula we use. But it’s easy to use and we’ll show you how.

To make it even easier, we’ve built a free online calculator for you, to help you find the total resistance of a parallel circuit.
You can find that HERE.

In a series circuit, the total resistance of the circuit was the resistance of each component just added together, why? Because the electrons had to pass through each one, so the more resistors they passed through, the more the total resistance increased.

However, with parallel circuits we’re providing lots of different paths for the electrons to flow through. So we instead work out how conductive each branch is, or how easy can electricity pass through each branch. We then combine these values and then convert it back into resistance.

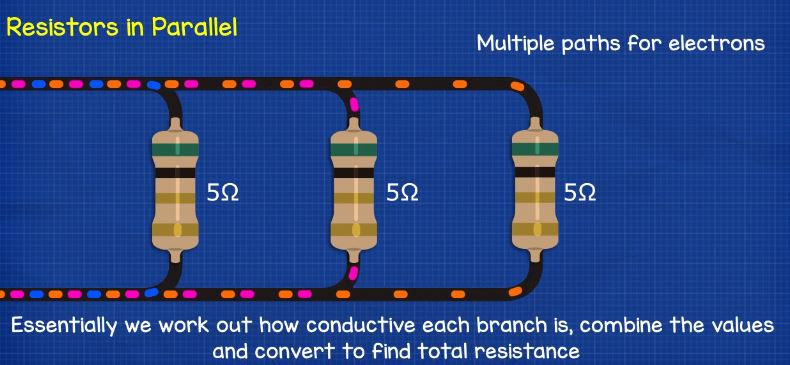
Lets take a simple parallel circuit with two 10 ohm resistors. How do we find the total resistance of the circuit?

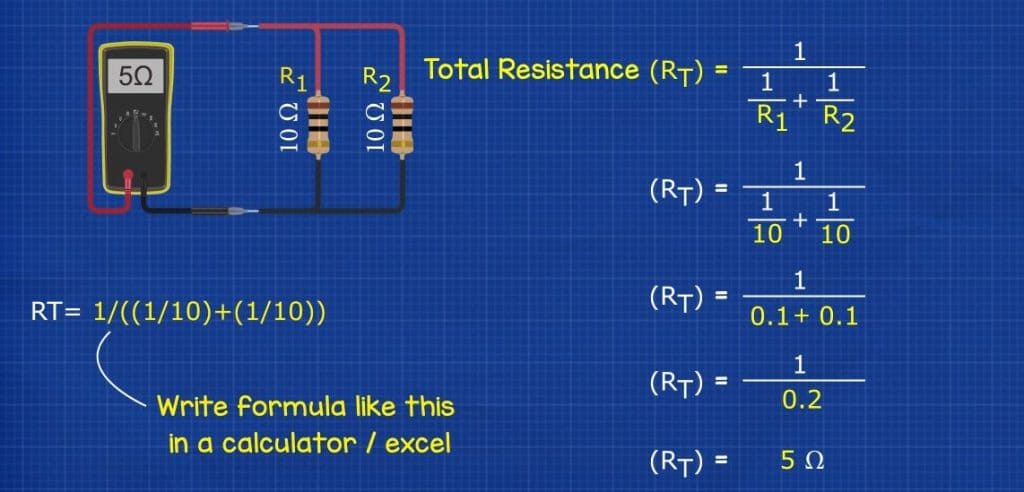
We use that formula, RT = 1 / 1/R1 + 1/R2. We then replace the R1 and R2 values with our resistor 1 and resistor 2 values. We start at the bottom, and we divide 1 by 10 ohms for both which gives us 0.1 + 0.1. So the formula has now reduced to 1 divided by 0.1 + 0.1 so we add the two decimals together to get 0.2, the formula is now 1 divided by 0.2 so then we divide 1 by 0.2 to get 5 ohms total resistance.
If you do this calculation on a calculator or excel then just remember to use your brackets.

So although we had two 10 ohm resistors, the total resistance is only 5 ohms. That’s because as the current has been split, the resistance has reduced. 

If we had two 5 ohm resistors then the total resistance is 2.5 ohms.

If we had a 10 and a 5 ohm resistor then the total resistance is 3.33 Ohms

If we have more resistors then we just keep adding them into the formula. For example three 10 ohm resistors gives us 1, divided by, 1 over R1 plus 1 over R2 plus 1 over R3. We input our resistor values and we get again 3.33 Ohms.

A 10ohm a 5 ohm and a 2 ohm resistor gives us 1.25 Ohms total resistance. 

Why are we using all these 1 divided by resistor fractions in the formula? You don’t really need to remember why we do it, you just need to remember the formula we use. But we’ll just explain briefly why we do it this way.

Because there are many paths for the current to flow through, so instead we work out how well electricity can pass through each path, that’s the conductance which is the opposite or reciprocal to resistance. As we already know the resistance values of the resistors, we can just invert the value to find the opposite. 

Looking at a 10 Ohm resistor we can also write 10 = 10 divided by 1. Because 10 divided by 1 is 10, and you can do that with any number. Then we invert the number to find the conductance or the reciprocal and we do that by flipping the denominator and the numerator. So we get 1 divided by 10, which is 0.1 

We can flip it back to resistance by again diving that by 1, because it’s the opposite. So 1 divided by 0.1 is 10.

If we had a 1 ohm resistor then we have a conductivity of 1. If we had a 1,000 ohm resistor we have a conductivity of 0.001 so you can see that it’s going to be easier for the electricity to pass through the 1 ohm resistor because it has better conductivity. 

So once we work out how conductive each path is, we add them together to find our total conductivity. We can convert that back to resistance by taking the reciprocal so 1 divided by the total conductance gives us our total resistance.

Power consumption in parallel circuits

The resistors and components will convert the electrical energy into thermal energy as the electrons collide inside the component. That’s why they become hot and we can see that with a thermal imaging camera.

So how much power are the individual components and the circuit in total consuming?

We can use two formulas for this, either: Voltage squared divided by resistance Or Voltage multiplied by current. Let’s see some examples.

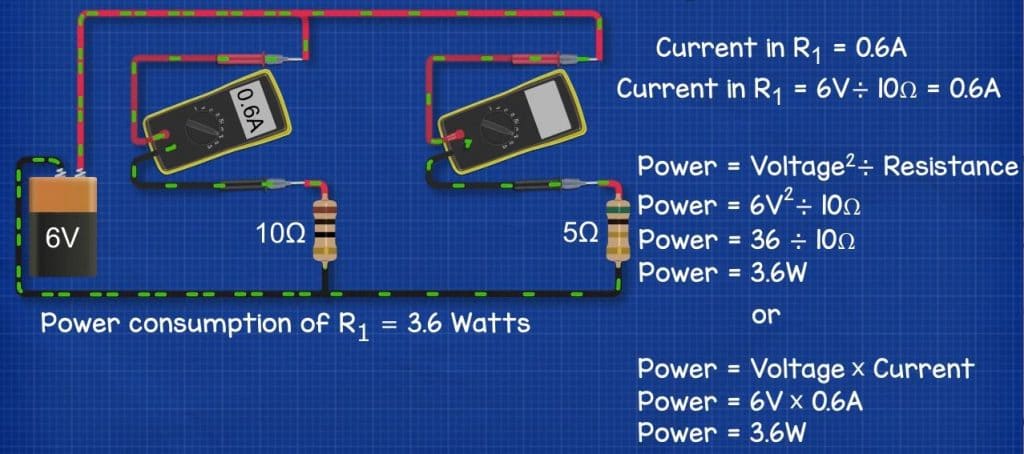
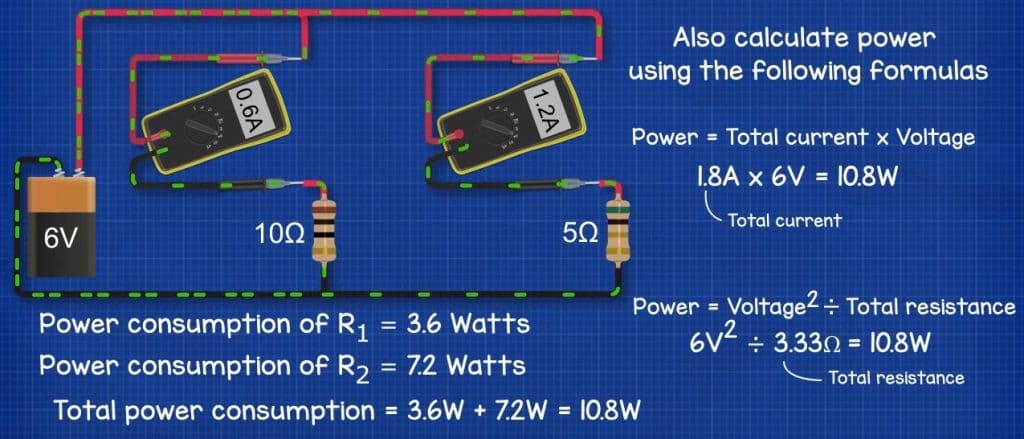
Say we have a 10 ohm and a 5 ohm resistor connected in parallel to a 6V battery. R1 has a current of 0.6A (That’s 6V / 10 Ohm = 0.6A) So the power consumption of the component is 3.6Watts. We see that from 6V^2 / 10 Ohm, 6V^2 = 36, so 36/10 is 3.6W. Alternatively 6V multiplied by 0.6A also gives us 3.6W

R2 is 5 ohms with a current of 1.2A (That’s 6v / 5 Ohm = 1.2A) so its power consumption is 7.2W. We see that from 6V^2 / 5 Ohm, 6V^2 = 36, so 36/5 is 7.2W. Alternatively 6V multiplied by 1.2A also gives us 7.2W

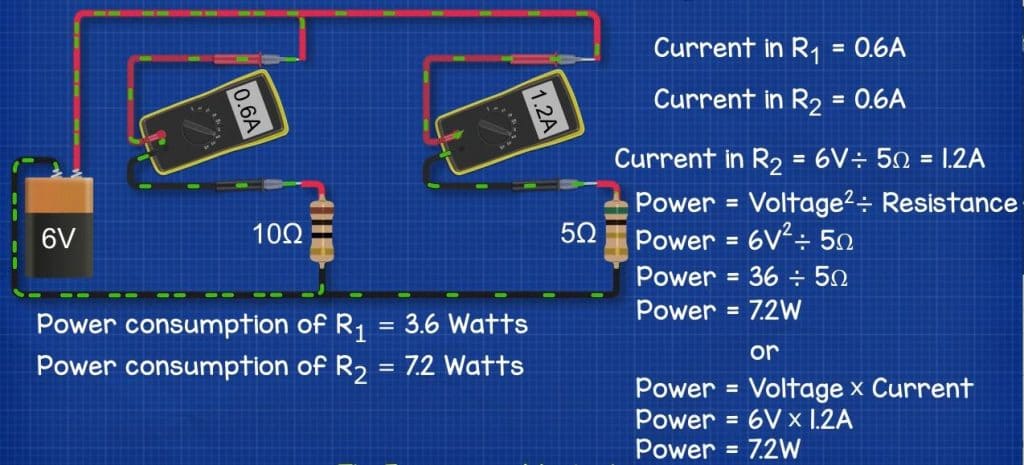
Total power consumption is therefore 3.6W + 7.2W which is 10.8W

We could have also found this by Multiplying the Voltage by the total current, the total current for this circuit is 1.8A so 6V multiplied by 1.8A is 10.8W

Or we could have used voltage squared divided by total resistance. The total resistance of this circuit is 3.33 Ohms so 6V squared is 36, divided by 3.33 Ohms is 10.8W

Problems and Solutions, Can You Solve?

Now lets see if you can solve these problems.

Question 1) We have four resistors in parallel. A 10 ohm, a 20 ohm, a 2 ohm and a 3 ohm. What is the total resistance of the circuit?

Answer

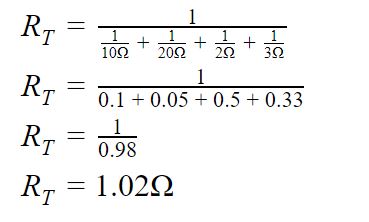
Question 2) We have three resistors connected in parallel to a 6V battery. The total current in the circuit is 2.5A, resistor 1 is 10 ohm with a current of 0.6A, resistor 2 is 15 ohm with an unknown current, and resistor 3 has an unknown resistance value and an unknown current. Calculate the current flowing in resistor 2 as well as the current and resistance of resistor 3.

Answer

First we find the current in resistor 2 using Ohms law. Current = Voltage divided by Resistance.
6V divided by 15 Ohms is 0.4A

Now we find the current in resistor 3 by subtracting the current of resistor 1 and resistor 2 from the total current. Total current is 2.5A subtract 0.6A and 0.4A gives us 1.5A flowing through resistor 3.

Now we find the resistance of resistor 3 using ohm’s law again. Resistance is voltage divided by current. So 6V divided by 1.5A gives us 4 Ohms resistance.

---