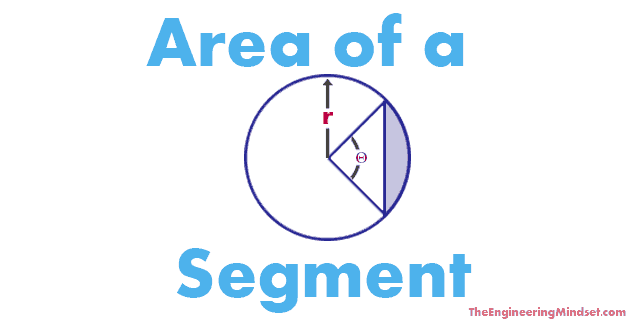
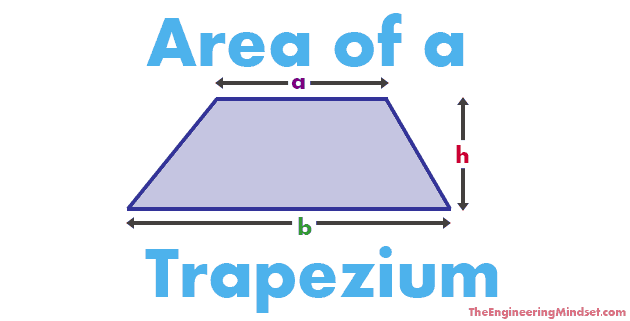
The area of a segment can be calculated using the following formula
If using degrees:
A = (r2 ÷ 2) x ((Π ÷ 180 x Θ) – sin Θ)
If using radians:
A = (0.5 x r2) x (Θ – sin Θ)
Where:
A = Area
r = Radius
Π = Pi (3.14)
Θ = Angle
0.5 = A constant
180 = A constant
Example (In Degrees)
You’ve been asked to calculate the area of a sector when the radius of the circle is 5m and the angle is 120 degrees.
A = (r2 ÷ 2) * ((Π ÷ 180 * Θ) – sinΘ)
A = (52 ÷ 2) * ((Π ÷ 180 * 120) – sin120)
A = (12.5) * ((Π ÷ 180 * 120) – sin120)
A = (12.5) * ((0.017453 * 120) – sin120)
A = (12.5) * ((0.017453 * 120) – sin120)
A = (12.5) * ((2.0944) – 0.866025)
A = (12.5) * (1.22837)
A = 15.35m2
Example (In Radians)
You’ve been asked to calculate the area of a sector when the radius of the circle is 5m and the angle is 2.094 radians. (Remember! put your calculator in radians)
A = (0.5 x r2) x (Θ – sin Θ)
A = (0.5 x 52) x (2.094 – sin 2.094)
A = (0.5 x 25) x (2.094 – sin 2.094)
A = (12.5) x (2.094 – sin 2.094)
A = (12.5) x (2.094 – 0.86622)
A = (12.5) x (2.094 – 0.86622)
A = (12.5) x (1.22778)
A = 15.35m2