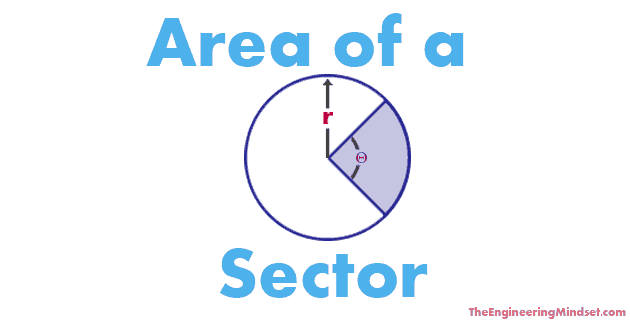
The area of a sector can be calculated with the following formula:
If calculated in degrees:
A = (Θ ÷ 360) x (Π x r2)
If calculated in radians:
A = 0.5 x r2 x Θ
Where
A = Area
Θ = Angle (measured in radians or degrees)
Π = Pi (3.14)
r = radius
360 = A Constant
0.5 = A Constant
Example (In Degrees)
You’ve been asked to calculate the area of a sector when the radius of the circle is 5m and the angle is 120 degrees.
r = 5m
Θ = 120
A = (Θ ÷ 360) x (Π x r2)
A = (120° ÷ 360) x (Π x 52)
A = (0.33333) x (Π x 25)
A = (0.33333) x (78.5398)
A = 26.18m2
First we divide the angle by 360. If the arc was a full circle, it would have 360 degrees, but because it is not a complete circle we need to know what percent of a circle it is. We do this by diving the angle by the total angle.
120 degrees ÷ 360 degrees = 0.3333 or 33.33% of a full circle
Then we calculated the area of the full circle using (Π x r2) and then multiplied the area of the full circle by the percent of the circle we actually have, to give us the area of the sector.
Example (In Radians)
You’ve been asked to calculate the area of a sector when the radius of the circle is 5m and the angle is 2.094 radians.
r = 5m
Θ = 2.094
A = 0.5 x r2 x Θ
A = 0.5 x 52 x 2.094
A = 0.5 x 25 x 2.094
A = 12.5 x 2.094
A = 26.18m2