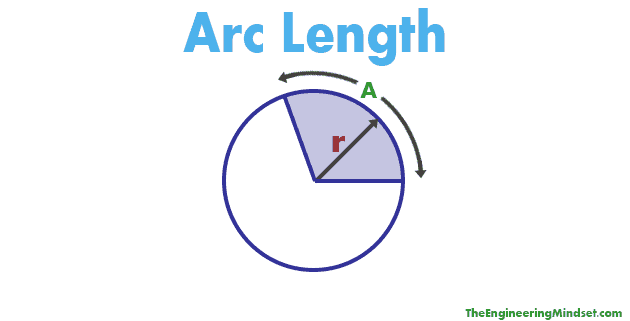
You can calculate the length of an arc quite simply, but how you calculate it depends if the angle of the arc is measured in degrees or radians.
Measured in degrees
If the angle of your arc is measured in degrees then use this formula to calculate the length of the arc:
Arc length (A) = (Θ ÷ 360) x (2 x π x r)
or
A = (Θ ÷ 360) x (D x π)
Where:
A = Arc length
Θ = Arc angle (in degrees)
r = radius of circle
D = Diameter of circle
Example
You’ve been asked to calculate the length of an arc when the radius of the circle is 5m and the angle is 120 degrees.
r = 5m
Θ = 120
First we divide the angle by 360. If the arc was a full circle, it would have 360 degrees, but because it is not a complete circle we need to know what percent of a circle it is. We do this by diving the angle by the total angle.
120 degrees ÷ 360 degrees = 0.3333 or 33.33% of a full circle
Next we calculate the circumference of the full circle. Click here to learn about how to calculate the circumference of a circle.
C = 2 x π x r
C = 2 x 3.142 x 5m
C = 6.284 x 5m
C = 31.42m
Now we just find what 33.3% of the circumference is
A = 0.3333 * 31.42m = 10.47m
Measured in radians
If the angle of your arc is measured in radians then use this formula to calculate the length of the arc:
A = r x Θ
Where:
A = length of arc
r = radius of circle
Θ = angle or arc (in radians)
Example
You’ve been asked to calculate the length of an arc when the radius of the circle is 5m and the angle is 2.094 radians.
r = 5m
Θ = 2.094 It’s pretty simple, just multiply the radius by the angle
A = 5m x 2.094 radians = 10.47m














[…] Arc length, how to calculate […]
There is certainly lots to learn on this topic. I like all the advice
you have given.
i had to look at so many sites before coming to this one and i actually understood how it works looking at this, ty
[…] Figure 6: Arc Length Source: https://theengineeringmindset.com/arc-length-how-to-calculate/ […]